
HL Paper 3
An observer A is on the surface of planet X. Observer B is in a stationary spaceship above the surface of planet X.
Observer A sends a beam of light with a frequency 500 THz towards observer B. When observer B receives the light he observes that the frequency has changed by Δf.
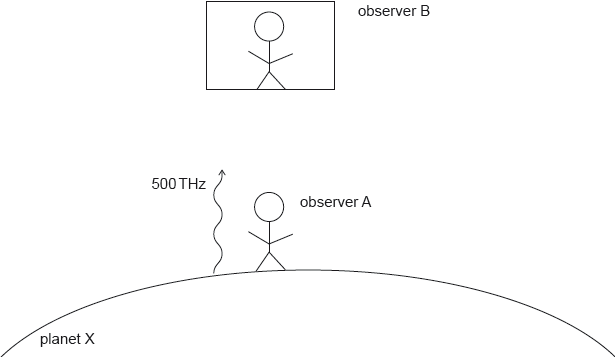
Observer B then sends a signal with frequency 1500 THz towards observer A.

Calculate the shift in frequency observed by A in terms of Δf.
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
Observer A now sends a beam of light initially parallel to the surface of the planet.
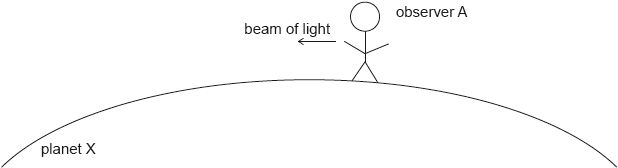
Explain why the path of the light is curved.
The \({\Lambda ^0}\) (Lambda) particle decays spontaneously into a proton and a negatively charged pion of rest mass 140 MeV c–2. After the decay, the particles are moving in the same direction with a proton momentum of 630 MeV c–1 and a pion momentum of 270 MeV c–1.
Determine the rest mass of the \({\Lambda ^0}\) particle.
Determine, using your answer to (a), the initial speed of the \({\Lambda ^0}\) particle.
This question is about general relativity.
Bob is standing on the floor of a spaceship and he throws a ball in a direction parallel to the floor.
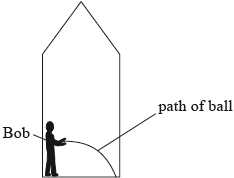
Between leaving Bob’s hand and landing on the floor, the ball follows the path shown.
State and explain whether, from the path followed by the ball, Bob can deduce that the spaceship is at rest on the surface of a planet.
Outline how the concept of spacetime can be used to explain the
(i) trajectory of the ball if the spaceship is at rest on the surface of a planet.
(ii) nature of a black hole.
Calculate the radius that Earth would have to have in order for it to behave as a black hole. The mass of Earth is \(6.0 \times {10^{24}}{\text{ kg}}\).
The global positioning system (GPS) uses satellites that orbit the Earth. The satellites transmit information to Earth using accurately known time signals derived from atomic clocks on the satellites. The time signals need to be corrected due to the gravitational redshift that occurs because the satellites are at a height of 20 Mm above the surface of the Earth.
The gravitational field strength at 20 Mm above the surface of the Earth is about 0.6 N kg–1. Estimate the time correction per day needed to the time signals, due to the gravitational redshift.
Suggest, whether your answer to (a) underestimates or overestimates the correction required to the time signal.
This question is about pair production and relativistic mechanics.
A \(\gamma \)-photon of energy 2.46 MeV is travelling close to the nucleus of a gold atom. It converts into an electron (\({{\text{e}}^ - }\)) – positron (\({{\text{e}}^ + }\)) pair. Each particle travels at 45° to the original direction of the photon.
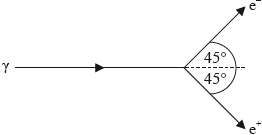
Immediately after the conversion, the kinetic energies of the electron and positron are equal. The magnitude of the recoil momentum of the gold nucleus is \(0.880{\text{ MeV}}\,{{\text{c}}^{ - 1}}\) and is in the direction of the photon.
Calculate, immediately after the decay, the magnitude of the momentum of the electron.
Calculate the value \(V\) of the potential difference through which an electron at rest must be accelerated in order to have the same magnitude of momentum as that in (a).
It is believed that a non-rotating supermassive black hole is likely to exist near the centre of our galaxy. This black hole has a mass equivalent to 3.6 million times that of the Sun.
Outline what is meant by the event horizon of a black hole.
Calculate the distance of the event horizon of the black hole from its centre.
Mass of Sun = 2 × 1030 kg
Star S-2 is in an elliptical orbit around a black hole. The distance of S-2 from the centre of the black hole varies between a few light-hours and several light-days. A periodic event on S-2 occurs every 5.0 s.
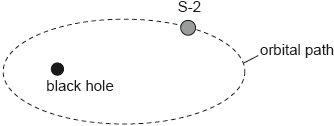
Discuss how the time for the periodic event as measured by an observer on the Earth changes with the orbital position of S-2.
This question is about a Galilean transformation and time dilation.
Ben is in a spaceship that is travelling in a straight-line with constant speed v as measured by Jill who is in a space station.
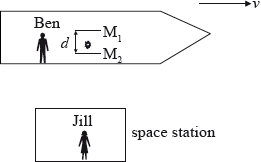
Ben switches on a light pulse that bounces vertically (as observed by Ben) between two horizontal mirrors \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{2}}}\) separated by a distance \(d\). At the instant that the mirrors are opposite Jill, the pulse is just leaving the mirror \({{\text{M}}_{\text{2}}}\). The speed of light in air is \(c\).
The questions (e) and (f ) introduce the concepts of time dilation and length contraction. Discuss how muon decay in the atmosphere provides experimental evidence for these concepts.
The Schwarzschild radius of a black hole is 6.0 x 105 m. A rocket is 7.0 x 108 m from the black hole and has a clock. The proper time interval between the ticks of the clock on the rocket is 1.0 s. These ticks are transmitted to a distant observer in a region free of gravitational fields.
Outline why the clock near the black hole runs slowly compared to a clock close to the distant observer.
Calculate the number of ticks detected in 10 ks by the distant observer.
An electron and a positron have identical speeds but are travelling in opposite directions. Their collision results in the annihilation of both particles and the production of two photons of identical energy. The initial kinetic energy of the electron is 2.00 MeV.
Explain, in terms of a conservation law, why two photons need to be created.
Determine the speed of the incoming electron.
Calculate the energy and the momentum for each photon after the collision.
A positive pion decays into a positive muon and a neutrino.
\[{\pi ^ + } \to {\mu ^ + } + {v_\mu }\]
The momentum of the muon is measured to be 29.8 MeV c–1 in a laboratory reference frame in which the pion is at rest. The rest mass of the muon is 105.7 MeV c–2 and the mass of the neutrino can be assumed to be zero.
For the laboratory reference frame
write down the momentum of the neutrino.
show that the energy of the pion is about 140 MeV.
State the rest mass of the pion with an appropriate unit.
In an experiment a source of iron-57 emits gamma rays of energy 14.4 ke V. A detector placed 22.6 m vertically above the source measures the frequency of the gamma rays.
Calculate the expected shift in frequency between the emitted and the detected gamma rays.
Explain whether the detected frequency would be greater or less than the emitted frequency.
This question is about relativistic dynamics.
A proton is accelerated from rest through a potential difference of 2.5 GV. Determine the momentum of the proton after acceleration.
Outline what is meant by a black hole.
An observer views a distant spacecraft that is 23.0 km from the centre of a black hole. The spacecraft contains a clock that ticks once every second and the ticks can be detected by the distant observer. In 2.00 minutes the observer counts 112 ticks of the clock.
Determine the mass of the black hole.
State what is meant by the event horizon of a black hole.
Show that the surface area A of the sphere corresponding to the event horizon is given by
\(A = \frac{{16\pi {G^2}{M^2}}}{{{c^4}}}\).
Suggest why the surface area of the event horizon can never decrease.
The diagram shows a box that is falling freely in the gravitational field of a planet.
A photon of frequency f is emitted from the floor of the box and is received at the ceiling. State and explain the frequency of the photon measured at the ceiling.
This question is about general relativity.
Calculate the Schwarzschild radius for an astronomical object of mass 5.0 ×1030 kg.
A spaceship is travelling towards the object in (a). The spaceship moves in a straight line such that its distance of closest approach would be about 107m. Discuss why the presence of the object in (a) will not significantly affect the motion of the spaceship.
An observer, when viewing a distant galaxy, sees two images of the galaxy separated by a small angle. A massive star is positioned between the observer and the galaxy. Outline how these observations give support to the theory of general relativity.
This question is about relativistic kinematics.
A spacecraft is flying in a straight line above a base station at a speed of 0.8c.
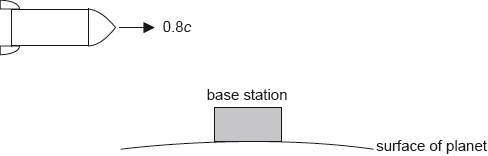
Suzanne is inside the spacecraft and Juan is on the base station.
State what is meant by an inertial frame of reference.
A light on the base station flashes regularly. According to Suzanne, the light flashes every 3 seconds. Calculate how often the light flashes according to Juan.
While moving away from the base station, Suzanne observes another spacecraft travelling towards her at a speed of 0.8c. Suzanne measures the other spacecraft to have a length of 8.00 m. Calculate the proper length of the other spacecraft.
Suzanne’s spacecraft is on a journey to a star. According to Juan, the distance from the base station to the star is 11.4 ly. Show that Suzanne measures the time taken for her to travel from the base station to the star to be about 9 years.
Suzanne then returns to the base station at the same speed. The total time since leaving the base station as measured by Suzanne is around 18 years but the total time according to Juan is around 29 years. Explain how it is possible for Suzanne and Juan to have aged by different amounts.
This question is about gravitation.
Planets move in orbits around the Sun. Explain this observation according to
Newton’s universal law of gravitation.
Einstein’s theory of general relativity.
This question is about relativistic kinematics.
An observer at rest relative to Earth observes two spaceships. Each spaceship is moving with a speed of 0.85c but in opposite directions. The observer measures the rate of increase of distance between the spaceships to be 1.7c.
(i) Outline whether this observation contravenes the theory of special relativity.
(ii) Determine, according to an observer in one of the spaceships, the speed of the other spaceship.
The observer on Earth in (a) watches one spaceship as it travels to a distant star at a speed of 0.85c. According to observers on the spaceship, this journey takes 8.0 years.
(i) Calculate, according to the observer on Earth, the time taken for the journey to the star.
(ii) Outline whether the time interval measured by the observer on Earth is a proper time interval.
(iii) Calculate, according to the observer on Earth, the distance from Earth to the star.
(iv) The observers in the spaceship send a message to Earth halfway through their journey. Determine how long it takes the message to arrive at Earth according to the observers on the spaceship.
This question is about relativistic momentum and energy.
An electron and a positron travel towards each other in a straight line in a vacuum. A positron is a positively charged electron.

The speed of each particle, as measured by an observer in the laboratory, is 0.85c. The value of the Lorentz factor at this speed is approximately 1.9.
The electron and positron annihilate each other, creating two photons in the process. Each of the photons transfers the same quantity of energy.
Calculate the speed of the positron as measured in the frame of reference of the electron.
Calculate the total energy in the reaction.
Outline why two photons must be released in this collision.
Determine the frequency of one of the photons.
This question is about muon decay.
Muons are produced in the Earth’s atmosphere at a height of around 10 km above the surface. They then travel at a speed of around 0.98c towards the Earth. The average time for a muon to decay is approximately \({\text{2.2 }}\mu {\text{s}}\), according to observers at rest relative to the muon.
Many muons are observed to reach the surface of the Earth.
Deduce that few muons would be expected to arrive at the surface of the Earth if non-relativistic mechanics are assumed.
Calculate the average decay time of a muon as observed by an observer on the surface of the Earth.
Explain, with a calculation, why many muons reach the surface of the Earth before they have decayed.
A proton is accelerated from rest through a potential difference V to a speed of 0.86c.
Calculate the potential difference V.
The proton collides with an antiproton moving with the same speed in the opposite direction. As a result both particles are annihilated and two photons of equal energy are produced.
Determine the momentum of one of the photons.
An electron is emitted from a nucleus with a total energy of 2.30MeV as observed in a laboratory.
Show that the speed of the electron is about 0.98c.
The electron is detected at a distance of 0.800 m from the emitting nucleus as measured in the laboratory.
(i) For the reference frame of the electron, calculate the distance travelled by the detector.
(ii) For the reference frame of the laboratory, calculate the time taken for the electron to reach the detector after its emission from the nucleus.
(iii) For the reference frame of the electron, calculate the time between its emission at the nucleus and its detection.
(iv) Outline why the answer to (b)(iii) represents a proper time interval.
This question is about spacetime.
Describe what is meant by spacetime.
State the shape of the path in spacetime of a body
(i) moving at constant velocity.
(ii) orbiting the Earth.
Explain how spacetime is used to describe the gravitational attraction between Earth and a satellite orbiting the Earth.
This question is about relativistic mechanics.
A proton, after acceleration from rest through a potential difference V, has momentum 1600MeVc–1.
Calculate the value of V.
This question is about relativistic energy and momentum.
A proton is accelerated from rest through a potential difference V. The proton reaches a speed of 0.970c. Determine the value of V.
Calculate, after acceleration for the proton in (a), its
(i) mass.
(ii) momentum.
This question is about relativistic energy and momentum.
A proton is accelerated from rest through a potential difference V. After acceleration the mass of the proton is equal to four times its rest mass. Determine the value of V.
For the proton in (a) calculate, after acceleration, its
(i) speed.
(ii) momentum.
This question is about the equivalence principle and black holes.
State the principle of equivalence.
The gravitational field strength near the surface of a neutron star is 1.2 ×1013Nkg–1. A light ray is emitted from a stationary probe at a height of 250 m above the surface. The frequency of the light measured in the probe is 4.8×1014 Hz.
(i) Determine the frequency of the light received at the surface of the star according to an observer at the surface.
(ii) Describe how gravitational red-shift leads to the concept of gravitational time dilation.
General relativity predicts the existence of black holes.
(i) State what is meant by a black hole.
(ii) Suggest two ways in which a black hole may be detected.
This question is about black holes.
A space probe is stationary in the gravitational field of a black hole.

The mass of the black hole is \(4.5 \times {10^{31}}{\text{ kg}}\). The space probe is emitting a pulse of blue light at a time interval of 1.0 seconds as measured on the space probe. The light is received by an observer on a distant space station that is stationary with respect to the space probe.
Explain why the light reaching the space station will be red-shifted.
The time between the pulses as measured by the observer on the distant space station is found to be 1.5 s. Calculate the distance of the space probe from the black hole.
This question is about relativistic mechanics.
Calculate the potential difference through which a proton, starting from rest, must be accelerated for its mass–energy to be equal to three times its rest mass energy.
Calculate the momentum of the proton after acceleration.
This question is about relativistic mechanics.
A proton, after acceleration from rest through a potential difference V, has momentum 1600MeVc–1.
Calculate the speed of the proton after acceleration.
Describe what is meant by spacetime.
Outline how the concept of spacetime accounts for the
(i) orbiting of Earth about the Sun.
(ii) nature of a black hole.
This question is about relativistic kinematics.
A short pulse containing many nuclei of a radioactive isotope is emitted from a source S in a laboratory. The nuclei have speed v = 0.920c as measured with respect to the laboratory.
The pulse arrives at a detector D. The detector is 250 m away as measured by an observer in the laboratory.
Calculate the time it takes the pulse to travel from S to D, according to
(i) an observer in the laboratory.
(ii) an observer Q moving along with the pulse.
Calculate the distance between the source S and the detector D according to observer Q.
A particular nucleus in the pulse decays by emitting an electron in the same direction as that of the nucleus. The speed of the electron measured in the laboratory is 0.985c.
Calculate the speed of the electron as measured by observer Q.
The laboratory observer and observer Q agree that by the time the pulse arrives at D, half of the nuclei in the pulse have decayed.
Outline, without further calculation, how this is evidence in support of time dilation.
A lambda \(\Lambda \)0 particle at rest decays into a proton p and a pion \({\pi ^ - }\) according to the reaction
\(\Lambda \)0 → p + \(\pi \)–
where the rest energy of p = 938 MeV and the rest energy of \(\pi \)– = 140 MeV.
The speed of the pion after the decay is 0.579c. For this speed \(\gamma \) = 1.2265. Calculate the speed of the proton.
This question is about general relativity.
The diagram shows monochromatic light of frequency \({f_0}\) being emitted from the base of a box towards an observer C at the ceiling of the box. The box is in free fall above the surface of the planet. Light of the same frequency is also emitted from the surface of the planet towards an observer P at rest above the surface of the planet.
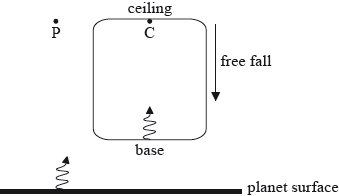
The frequency of the light as measured by C is \({f_{\text{C}}}\) and the frequency of the light as measured by P is \({f_{\text{P}}}\).
State and explain whether the frequencies \({f_{\text{C}}}\) and \({f_{\text{P}}}\) are less than, equal to or greater than \({f_0}\).
(i) \({f_{\text{C}}}\)
(ii) \({f_{\text{P}}}\)
Newton explained the motion of a planet around the Sun in terms of a force of gravitation between the Sun and the planet. Describe how Einstein’s theory of general relativity explains the motion of the planet around the Sun.
This question is about relativistic mechanics.
Show that the speed v of a particle of total energy E and momentum p is given by the following equation.
\[v = \frac{{p{c^2}}}{E}\]
Determine, using the answer in (a), the speed of a particle whose rest mass is zero.
This question is about general relativity.
A spacecraft is at rest on the surface of a distant planet. A laser beam is fired from the base
of the spacecraft to a sensor at the top of the spacecraft.
The spacecraft has a height of 112 m. The laser beam emitted from the source has a frequency of \(4.52 \times {10^{14}}{\text{ Hz}}\) and the sensor detects a shift in the frequency of the laser beam of 3.20 Hz.
Show that the gravitational field strength at the surface of the planet is about \({\text{5.7 N}}\,{\text{k}}{{\text{g}}^{ - 1}}\).
Discuss the shift in frequency of the laser beam.
The spacecraft leaves the planet with an acceleration of \({\text{5.7 m}}\,{{\text{s}}^{ - 2}}\). The same experiment is carried out by firing the laser beam from the base of the spacecraft to the sensor at the top of the spacecraft. Compare the shift in frequency of the laser beam with that detected in (a).
This question is about mass and energy.
The positive kaon \({K^ + }\) has a rest mass of \(494{\text{ MeV}}\,{{\text{c}}^{ - 2}}\).
Using the grid, sketch a graph showing how the energy of the kaon increases with speed.
The kaon is accelerated from rest through a potential difference so that its energy becomes three times its rest energy. Calculate the potential difference through which the kaon was accelerated.
The neutral kaon is unstable and one of its possible modes of decay is
\[{K^0} \to {\pi ^0} + {\pi ^0}.\]
The \({\pi ^0}\) has a rest mass of \(135{\text{ MeV}}\,{{\text{c}}^{ - 2}}\). The \({K^0}\) has a rest mass of \(498{\text{ MeV}}\,{{\text{c}}^{ - 2}}\). The \({K^0}\) is at rest before it decays. The two \({\pi ^0}\) particles move apart in opposite directions along a straight line. Determine the momentum of one of the \({\pi ^0}\) particles.
This question is about relativistic mechanics.
A proton is accelerated from rest through a potential difference of 1.5 GV.
Calculate, for the accelerated proton, the
total energy.
momentum.
speed.
This question is about relativistic mechanics.
A rho meson \((\rho )\) decays at rest in a laboratory into a pion \(({\pi ^ + })\) and an anti-pion \(({\pi ^ - })\) according to
\(\rho \to {\pi ^ + } + {\pi ^ - }\).
The rest masses of the particles involved are:
\({m_{{\pi ^ + }}} = {m_{{\pi ^ - }}} = 140{\text{ MeV}}\,{{\text{c}}^{ - 2}}\)
\({m_\rho } = \) \(770{\text{ MeV}}\,{{\text{c}}^{ - {\text{2}}}}\)
(i) Show that the initial momentum of the pion is \(360{\text{ MeV}}\,{{\text{c}}^{ - {\text{1}}}}\).
(ii) Show that the speed of the pion relative to the laboratory is 0.932c.
(iii) Calculate, in \({\text{MeV}}\,{{\text{c}}^{ - 2}}\), the mass that has been converted into energy in this decay.
The pion \(({\pi ^ + })\) emits a muon in the same direction as the velocity of the pion. The speed of the muon is 0.271c relative to the pion. Calculate the speed of the muon relative to the laboratory.
This question is about relativistic dynamics.
A proton is accelerated from rest by a potential difference V and reaches a speed of 2.5×108 m s–1. Calculate V.
This question is about rest mass and relativistic energy.
(i) Define the rest mass of a particle.
(ii) The rest mass of a particle is said to be an invariant quantity. State, with reference to special relativity, what is meant by the term invariant.
In a thought experiment, two particles X and Y, each of rest mass 380 MeVc–2, are approaching each other head on.
The speed of X and of Y is 0.60 c relative to a laboratory.
(i) Calculate the momentum of X in the frame of reference in which Y is at rest.
(ii) As a result of the collision a single particle Z is formed. Determine the rest mass of Z. The gamma factor for a speed of 0.60 c is 1.25.
This question is about relative velocities and energy at relativistic speeds.
Two identical rockets are moving along the same straight line as viewed from Earth. Rocket 1 is moving away from the Earth at speed 0.80 c relative to the Earth and rocket 2 is moving away from rocket 1 at speed 0.60 c relative to rocket 1.
Calculate the velocity of rocket 2 relative to the Earth, using the
(i) Galilean transformation equation.
(ii) relativistic transformation equation.
Comment on your answers in (a).
The rest mass of rocket 1 is 1.0×103kg. Determine the relativistic kinetic energy of rocket 1, as measured by an observer on Earth.
Two protons, travelling in opposite directions, collide. Each has a total energy of 3.35 GeV.
As a result of the collision, the protons are annihilated and three particles, a proton, a neutron, and a pion are created. The pion has a rest mass of 140 MeV c–2. The total energy of the emitted proton and neutron from the interaction is 6.20 GeV.
Calculate the gamma (γ) factor for one of the protons.
Determine, in terms of MeV c–1, the momentum of the pion.
The diagram shows the paths of the incident protons together with the proton and neutron created in the interaction. On the diagram, draw the path of the pion.
This question is about spacetime.
Explain, with reference to the warping of spacetime, the gravitational attraction between Earth and the Sun.
This question is about muon decay experiments.
Muons created high in the atmosphere move vertically down towards the surface of Earth. A muon detector T is placed on top of a mountain and another, detector S, is placed at sea level.
Detector T detects 570 muons per hour. In the rest frame of the muons their half-life is 1.5 μs. According to an observer, at rest on the mountain, the muons take 6.0 μs to travel from detector T to detector S.
Show that, if the muons move at non-relativistic speed, the number of muons detected at sea level would be approximately 36 per hour.
The muons in (a) move toward the surface of Earth with a relativistic speed of 0.968c.
(i) Determine the half-life of the muons according to the observer at rest on the mountain.
(ii) The number of muons observed at detector S is 285 per hour. Explain, using your answers to (a) and (b)(i), how this observation provides evidence for time dilation.
This question is about relativity.
Carrie is in a spaceship that is travelling towards a star in a straight-line at constant velocity as observed by Peter. Peter is at rest relative to the star.
Carrie and Louise, two observers in a spaceship, view a light source placed close to Carrie. When the spaceship is travelling at a constant velocity, they both measure the frequency of the light source and obtain identical values.
The magnitude of the velocity of the spaceship increases.
State and explain any changes to the frequency of the light source, as measured by Louise, that occur during the acceleration.
This question is about mass and energy.
The graph shows the variation with the fraction \(\frac{v}{c}\), of the kinetic energy EK of a particle, where v is the speed of the particle.
Determine, using the value EK =360 MeV from the graph, the rest mass of the particle in MeV c–2.
Determine, using data from the graph, the potential difference required to accelerate the particle in (a) from a speed of 0.63c to a speed of 0.96c. The charge of the particle is +e.
This question is about gravitational red-shift.
An observer is in a space capsule moving at a constant speed in the absence of gravitational fields.
A monochromatic source of gamma rays is fixed to the rear wall of the capsule. An observer at the other end of the capsule measures the frequency of the gamma rays.
The capsule now starts to decelerate.
Deduce the change in the frequency of the gamma rays, as measured by the observer, when the deceleration begins.
Outline, with reference to the principle of equivalence, how the situation in (a) relates to the concept of gravitational red-shift.
This question is about black holes.
Sirius B has a mass of 2.0×1030 kg.
Calculate the minimum density required for Sirius B to become a black hole in the future.
This question is about the equivalence principle.
State the equivalence principle.
The diagram shows two identical boxes in two different states of motion.
In diagram 1 the box is in free fall close to the surface of a planet. In diagram 2 the box is accelerating in a region of space far from other masses.
A ray of monochromatic light is emitted from the base B of each box and is received at the top T of each box.
Observers at B measure the frequency of the emitted light to be ƒ0.
State and explain, for each state of motion in diagram 1 and 2, if the frequency of light measured by an observer at T will be less than, equal to or greater than ƒ0.
Radio signals, sent at the same time from Earth, reflect off two satellites X and Y as shown. The satellites are at the same distance from Earth.
The signal from Earth to satellite X and the reflected signal pass close to the Sun.
Compare, using the theory of general relativity, the arrival times at Earth of the signal from X and the signal from Y.
This question about general relativity.
State the principle of equivalence.
A gamma-ray photon is emitted from the base of a tower towards the top of the tower.
(i) Explain, using the principle of equivalence, why the frequency of the photon as measured at the top of the tower is less than that measured at the base of the tower.
(ii) The frequency of the photon at the base is 3.5×1018 Hz and the tower is 23 m high. Determine the shift Δf in the frequency of the photon at the top of the tower.
(iii) Suggest, using your answer to (b)(ii), why the photon frequency must be measured very precisely for this experiment to be successful.
This question is about black holes.
The diagram shows the path of a light ray in the space around a black hole.
The radius of the dotted circle is the Schwarzschild radius of the black hole.
Define the Schwarzschild radius of a black hole.
Explain, using the concept of spacetime, why the path of the light ray is straight at distances far from the black hole and curved when near the black hole.
This question is about relativistic mechanics.
In an experiment at CERN in 1964, a neutral pion moving at a speed of 0.99975c with respect to the laboratory decayed into two photons. The speed of each photon was measured with respect to the laboratory.
Describe how the result of this experiment provided support for special relativity.
In another experiment, a neutral pion moving at 0.80c relative to a laboratory decayed into two photons as shown in the diagram.
Photon R moved in the direction of the pion and photon L in the opposite direction. The rest mass of the pion is 135 MeVc–2.
According to a laboratory observer,
(i) determine the total energy of the pion in MeV.
(ii) determine the momentum of the pion, in MeVc–1.
(iii) state and explain which photon, R or L, has the greater energy.
This question is about relativistic kinematics.
Speedy is in a spacecraft being chased by Police Officer Sylvester. In Officer Sylvester’s frame of reference, Speedy is moving directly towards Officer Sylvester at 0.25c.
Officer Sylvester switches on the blue flashing lamps on his police spacecraft.
(i) Calculate, assuming that a Galilean transformation applies to this situation, the value of the speed of the light that Speedy would measure using the flashing lamps.
(ii) Speedy measures the speed of the light emitted by the flashing lamps. Deduce, using the relativistic addition of velocities, that Speedy will obtain a value for the speed of light equal to c.
This question is about general relativity.
State the principle of equivalence.
An observer in a spaceship moving at constant speed measures the frequency f0 of light emitted by a source. The spaceship now accelerates to the right.
The observed frequency changes to f.
(i) Outline why, during the acceleration, f is less than f0.
(ii) Explain how the result outlined in (b)(i) leads to the deduction that time dilates near a planet.
This question is about gravitational red-shift.
Two identical lasers are situated on the surface of the Earth. One is directed horizontally towards observer A, who measures the frequency to be 4.62×1014Hz. The other is directed vertically upwards towards observer B, who is at a height of 1.00×102m.
(i) State how the frequency as measured by observer B compares with the frequency as measured by observer A.
(ii) Calculate the difference in frequency between the laser light as measured by observers A and B.
(iii) State one assumption that you made in (a)(ii).
The lasers are now placed on a spaceship, which is accelerating upwards at a constant rate of 9.81ms−2, far away from any other masses as shown below. The distance of observer D from the laser is 1.00×102m. Observer C is at the bottom of the spaceship.
Explain, with reference to the equivalence principle, the frequencies measured by observers C and D, as compared to observers A and B.
This question is about time dilation and relativistic mass.
Two space stations X and Y are at rest relative to each other. The separation of X and Y as measured in their frame of reference is 1.80×1011m.
State what is meant by a frame of reference.
A radio signal is sent to both space stations in (a) from a point midway between them. On receipt of the signal a clock in X and a clock in Y are each set to read zero. A spaceship S travels between X and Y at a speed of 0.750c as measured by X and Y. In the frame of reference of S, station X passes S at the instant that X’s clock is set to zero. A clock in S is also set to zero at this instant.
(i) Calculate the time interval, as measured by the clock in X, that it takes S to travel from X to Y.
(ii) Calculate the time interval, as measured by the clock in S, that it takes S to travel from X to Y.
(iii) Explain whether the clock in X or the clock in S measures the proper time.
(iv) Explain why, according to S, the setting of the clock in X and the setting of the clock in Y does not occur simultaneously.
The spaceship S in (b) is moving with speed 0.750c as measured by X and Y and has a total energy of 2.72×1020J as measured by X and Y.
(i) Determine the rest mass of spaceship S.
(ii) Using the axes, sketch a graph to show how the mass m of spaceship S changes with its speed v. Your graph should identify the rest mass m=m0 and the speed v=c.
Muons are produced in the upper atmosphere of Earth and travel towards the surface of Earth where they are detected. Explain how, with reference to the situation described in (b), the production and detection of muons provide evidence for time dilation.
This question is about the principle of equivalence and red-shift.
Joe and Kim are travelling in a spaceship.
Joe is next to a light source L1 and Kim is next to an identical light source L2.
The acceleration of the spaceship is zero. Kim measures the frequency of the light from L1 to be the same as the frequency of the light from L2.
Outline why, if the spaceship now accelerates, Kim will measure the light from L1 to be red-shifted with respect to the light from L2.
Suggest, with reference to Einstein’s principle of equivalence, how your answer to (a) leads to the idea that a clock near a massive body runs more slowly than a clock in free space.
This question is about stellar distances and stellar properties.
According to Vladimir, a clock at rest in the railway carriage will appear to run slower than a clock at rest beside him. However, according to Natasha, Vladimir’s clock will run slower than a clock at rest beside her.
(i) Outline how this time dilation phenomenon leads to the “twin paradox” in which one of the twins embarks on a return journey to a distant star at a speed close to that of light whilst the other twin remains on Earth.
(ii) State the reason behind the resolution of the paradox.
Evidence for time dilation comes from the decay of muons. A pulse of muons produced by cosmic radiation in the upper atmosphere of Earth travels to Earth with a speed of 0.96c as measured by an observer at rest on the surface of Earth. The half-life of the muons, as measured in the frame of reference in which the muons are at rest, is 3.1×10–6s.
(i) Determine for the muons, the distance that Earth will have travelled towards them after half of the muons in the pulse have decayed.
(ii) Calculate for the Earth observer, the distance that the muon pulse will have travelled towards Earth after half of the muons in the pulse have decayed.
Suggest how your answers to (e)(i) and (e)(ii) provide evidence that supports the theory of special relativity.
This question is about general relativity.
State the equivalence principle.
A helium filled balloon is floating in air inside a spacecraft in outer space. The spacecraft begins to accelerate to the right.
Explain, with reference to the equivalence principle, the motion, if any, of the helium balloon relative to the spacecraft.
In an experiment, to verify the bending of light as it passes close to the Sun, the position of a star was measured during a total solar eclipse.
(i) Explain why the measurement of the star’s position was made during a total solar eclipse.
(ii) On the diagram above, draw lines to determine the apparent position of the star as seen from Earth.
(iii) State what other measurement must be made in order to determine the angle by which rays from the star are bent by the Sun.
(iv) The angle of bending of a light ray from the star that just grazes the Sun’s surface is θ. State and explain the effect, if any, on θ if the Sun were to be replaced by another star of equal radius but larger mass.
This question is about relativistic kinematics.
In a thought experiment, a train is moving at a speed of 0.950c relative to the ground. A pendulum attached to the ceiling of the train is set into oscillation.
An observer T on the train and an observer G on the ground measure the period of oscillation of the pendulum.
Observer G sees a second train moving towards the first train (i.e. towards the left) at a speed of 0.950c with respect to the ground. Calculate the relative speed of the trains.
This question is about general relativity.
A rocket is in outer space far from all masses. It moves along the dotted line according to an inertial observer located outside the rocket.
A ray of light is moving at right angles to the direction of the rocket according to the same inertial observer. The ray of light enters the rocket through a window W. Draw the path of the light ray according to an observer at rest inside the rocket,
(i) when the rocket is moving at constant speed v.
(ii) when the rocket is moving at constant positive acceleration a.
The acceleration of the rocket in (a)(ii) is 12ms–2. A gamma ray is emitted from the base of the rocket. The frequency at the base is fbase= 3.4×1018Hz. A detector in the rocket is at a distance of 25m above the base. The frequency measured by the detector is fdetector. Determine the frequency shift fdetector–fbase.
This question is about evidence that supports general relativity.
The astronomical photograph taken from Earth shows four separate images of a single distant quasar that appear to surround a galaxy. The galaxy is closer to Earth than the quasar.
Outline how one image of the quasar is formed. You may draw on the diagram below that shows the arrangement of the Earth, the galaxy and the quasar to support your answer.
This question is about relativistic energies.
Calculate the speed of an electron when its total energy is equal to five times its rest mass energy.
The electron is accelerated from rest through a potential difference V. The graph shows how the speed v of the electron after acceleration varies with V assuming that Newtonian mechanics applies.
On the graph, sketch a line to show the variation with V of v according to relativistic mechanics.
An observer on Earth watches two rockets, A and B. The spacetime diagram shows part of the motion of A and B in the reference frame of the Earth observer. A and B are travelling in the same direction.
For the reference frame of the Earth observer, calculate the speed of rocket A in terms of the speed of light c.
One rocket passes the other at event E. For the reference frame of the Earth observer, estimate
(i) the space coordinate of E, in kilometres.
(ii) the time coordinate of E, in seconds.
Three flashing light beacons, X, Y and Z, are used to guide another rocket C. The flash events are shown on the spacetime diagram. The diagram shows the axes for the reference frames of Earth and of rocket C. The Earth observer is at the origin.
Using the graph opposite, deduce the order in which
(i) the beacons flash in the reference frame of rocket C.
(ii) the Earth observer sees the beacons flash.